GSoC/2021/StatusReports/TanmayChavan: Difference between revisions
| Line 99: | Line 99: | ||
However, it has bugs. It is not perfectly commutative. One order of selection will produce incorrect results, but a different order will produce the correct results. This could lead to missing edges or some extra lines. There are some issues while clipping curves with polygons drawn using polyline tool. However, as these issues do not occur with rectangle tool, these are most certainly bugs, and the algorithm works.<br> | However, it has bugs. It is not perfectly commutative. One order of selection will produce incorrect results, but a different order will produce the correct results. This could lead to missing edges or some extra lines. There are some issues while clipping curves with polygons drawn using polyline tool. However, as these issues do not occur with rectangle tool, these are most certainly bugs, and the algorithm works.<br> | ||
[[File:Screenshot from 2021-08-20 17-22-40.png|frameless|center|incorrect clipping, before]] | |||
[[File:Screenshot from 2021-08-20 17-22-50.png|frameless|center|wrong clipping]] | |||
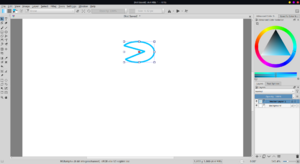
But, if we reselect the shapes, the clipping works as expected | |||
[[File:Screenshot from 2021-08-20 17-22-36.png|frameless|center|correct clipping due to different order of selection]] | |||
<br>However, as most of the operations do work one way or the other, I guess the algorithm is sound. With some extra time and effort it will produce the correct results. However, given more time, one of the two aforementioned approaches will be a better fit for our purposes as they tend to be cleaner without so many conditions and need for treating the special cases differently. | |||
However, as most of the operations do work one way or the other, I guess the algorithm is sound. With some extra time and effort it will produce the correct results. However, given more time, one of the two aforementioned approaches will be a better fit for our purposes as they tend to be cleaner without so many conditions and need for treating the special cases differently. | |||
== Ways to complete the remaining task == | == Ways to complete the remaining task == | ||
Revision as of 12:00, 20 August 2021
Krita - Smarter boolean operations on vector shapes
In Krita, performing boolean operations on vector shapes leads to a large number of unnecessary nodes. This happens because Qt lacks a proper algorithm to find the intersection point of two Bezier curves. I plan on implementing a numerically stable as well as efficient algorithm to find the intersections of two Bezier curves.
Mentors
- Dmitry Kazakov
- Iván Santa María
Goals
- Create a new algorithm to compute intersections of Bezier curves using implicitization
- done!
- Manage the dependencies and implement parts of Qt private modules in Krita codebase
- done!
- Integrate the algorithm with current intersection finding routine
- done!
- Implement the new routine for boolean operations
- not fully done
- Write proper documentation and unit tests for all the above goals while doing them
- ongoing
Status Report
Algorithm for Bezier curve intersection
- This was the exact feature which Qt lacked for boolean operations. As a result, it flattened the curves which in turn made too many nodes. I have implemented an algorithm to compute the intersection points using the implicit representation of a cubic Bezier curve. I have finished implementing curve-curve, line-curve intersections by now. The algorithm works well even with double precision. But, the curve-curve intersections can get really costly. On an average, a single curve-curve intersection-finding routine requires ~280 microseconds. However, it is reported this is the fastest method for curves with degree 5 or less. The line-line intersection point is obtained in the same manner as Qt did.
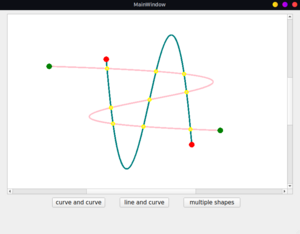
- Relevant links:
- Phabricator task: https://phabricator.kde.org/T14679
- Relevant MRs: https://invent.kde.org/earendil/bezierintersections (Due to the nature of the project, the code can only be merged with Krita codebase upon the entire task being done. Because of this, I have added my work in a seperate toy Qt project which also provides a simple graphic view of the progress until now.)
- Blog post: https://tanmay-chavan.github.io/jasper-blog/jekyll/update/2021/07/13/gsoc-update.html
Qt private dependencies
- As the set operations were handled by the class QPathClipper which lies behind the Qt API, I had to manage the dependencies so that the new implementation would not rely on Qt private modules. This was relatively easy as QPathClipper was fairly independent and it's dependencies didn't have too many dependencies. I also managed to get a downstream copy of the QPainterPath class, albeit had to skip some parts (the PathStroker related part) as it was too closely linked to other Qt private modules. However, it was not required for the purpose of the current tasks. So, I have managed to get the project to run without any private or additional dependencies.
- Relevant links:
- Relevant MRs: https://invent.kde.org/earendil/bezierintersections
- Relevant MRs: https://invent.kde.org/earendil/bezierintersections
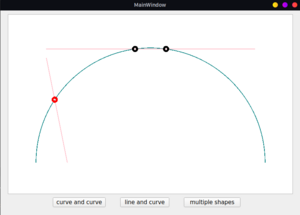
Intersection finding routine
- For this, I am using a downstream copy of QPainterPath. The elements of QPainterPaths are extracted and stored in the local version of PainterPath. After this, two vectors for subject shape and clip shape are created, where elements are added with the classes CubicBezier or Line as per the type of elements. Then, it proceeds to find the intersection points between the elements of the two vectors. These are stored in a separate class member with some additional information which could be helpful to perform set operations.
- Relevant links:
- phabricator task: https://phabricator.kde.org/T14681
- Relevant MRs: https://invent.kde.org/earendil/bezierintersections
Shape-clipping algorithm
Clipping proved to be a challenge, and I had initially underestimated it. Most of the problems arose as a suitable implementation was not available online, at least in FOSS. Most of them relied on flattening of the curves, much like Qt's algorithm. The wiki page mentioned Greiner-Hormann algorithm as one possibility for handling clipping for shapes with curves. However, there was no implementation available online. There were also several degenerate cases in Greiner-Hormann. It would fail if the two shapes had common vertices. It will also fail for common/overlapping edges, and for points of intersection lying on the vertices. The solution suggested was to change the co-ordinates of such problematic points. However this might lead to unexpected and undesired results. There is an improved version proposed, but the preprocessing routines were complicated and still had a few drawbacks. If there were a point of intersection coinciding with a point of self-intersection, the shape should be divided into several smaller non-intersecting shapes. Another major issue was that we needed to know at least one vertex of one shape lying outside the other shape. This is implemented in Qt, but within it's API, and works only for lines. (Currently, this can be implemented by using the tight bounding box function, and using an even-odd approach instead of Qt's winding-number approach.)
Apart from this, there was always an uncertainty as it had not been done before. There could be several problems there which remain unknown rill it is implemented. For this reason, I chose not to continue with that approach. However, I am writing down everything that has been done, what remains to be done, and how to do it should one choose to follow this approach.
For the latter approaches, the algorithm to split the shapes is crucial. Basically, until now, all of the intersection points between the two shapes can be found. The next task would be to process these shapes and select the edges which should be there in the final shape. Here, the splitting comes in play. We split all the elements of the shape about all of the intersection points. Thus, we get a shape which contains all of the segments in such a way that they need not be split again. Essentially, the final shape will consist of curves and lines exactly as in the splitted shapes, as they can't be split any further. This is half of the clipping job done; we have successfully marked the intersections and have generated a structure to readily traverse. The only job remaining is to choose which segments (lines or curves) should make it to the final shape.
This process makes it feasible to use Qt's algorithm for clipping it. Qt flattens the curves to process it, but preserves the end points. Since all of the intersection points are converted to end-points, they will remain as they are, without any loss in accuracy. This also makes it possible for us to resubstitute the curves after we flatten them, to obtain the original curves. Also, this covers two out of three steps required for Greiner-Hormann: finding all points of intersection and then processing the vertices while marking them correctly. After finding out at least one point lying outside the other shape, the only thing remaining is to select the segments to be added to the final shape.
My second approach was to carry out the process by modifying Qt's original algorithm. The basic idea is to mark the segments while flattening the curves, and then to restore the curves again when the WingedEdge structure is converted back to QPainterPath. The code is implemented. However, I was not able to fully finish it. The original code was complex, and was largely undocumented. I have implemented the marking and substitution process. However, there seems to be a bug introduced which causes the shapes to be improperly clipped. the fault mostly lies in the functions QWingedEdge::doClip and QWingedEdge::handleCrossingEdges. Debugging messages reveal the splitted edges are received correctly by doClip, but it decides not to select them. It could also lie in the `traverse` function, as it decides upto which edge should be considered. However, I was not able to debug it properly, due to limited time at hand. Given some more time, I'm pretty sure I'll be able to get it to work. However, I have documented Qt's code to the best of my capacity, and I hope it will quicken the process of understanding it's algorithm. The algorithm needs some time to be understood, and once understood, it can be corrected easily. Due to the time constraint, I stopped debugging it, and went to the third - and current - approach; to explicitly substitute the curves.
The final and current approach is to carry out the substitution routine outside Qt's clipping algorithm. After finding all points of intersection, we process the shapes to convert all points of intersection to regular vertices (in the function KisIntersectionFinder::processShapes.) Then we record all the clipped curves with the help of the class ``CubicBezierData``. Then, we clip the paths by Qt's own algorithm, without modifying it. Then, we traverse the final QPainterPath, and find the segments which are supposed to represent the flattened curve. As discussed above, the end points remain the same before and after flattening. Thus, we can find out a chain of continuous line segments (or ``lineTo`` elements) and if the end points of this chain match the end-points of one of the curves we have recorded, we replace the chain with the curve. This algorithm is the one being currently employed. It works for the union, intersection, subtraction operations for most of the cases.
Links
- MR link: https://invent.kde.org/graphics/krita/-/merge_requests/1002
- Blog: https://tanmay-chavan.github.io/jasper-blog/
- Project repo: https://invent.kde.org/earendil/bezierintersections (master branch)
- Phabricator task: https://phabricator.kde.org/T14574
Completed Tasks
- I have managed to write the code to find points of intersection of curves with curves, lines with curves, and integrate it with line-line intersection finding routine.
- I have managed all the private Qt dependencies needed for the project by creating copies of private QT programs in the Krita codebase, and integrated them successfully.
- I have written the classes needed to handle intersections of two `QPainterPaths` and then process them by splitting them about their intersection points.
- I have written documentation for the programs I have written and added some for the copied Qt files. I have also written unit tests for my code.
Task partially done
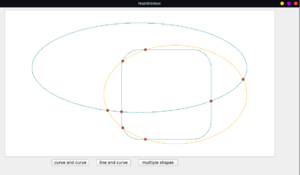
I have not implemented the clipping correctly. The current algorithm (in ``KisIntersectionFinder::resubstituteCurves()``) is able to produce valid results for some shapes, for union, intersection, and difference operation. Apart from the basic shapes, it also works for all of the tools (freehand curves, Bezier tool).
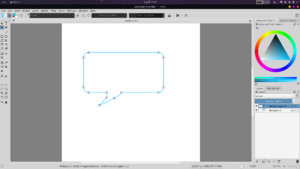
Operations with multiple shapes also work.
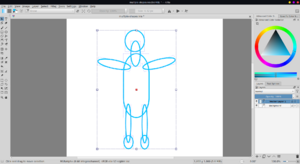
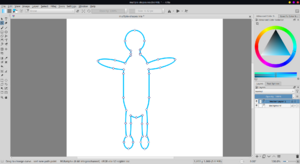
The freehand path tool also works.
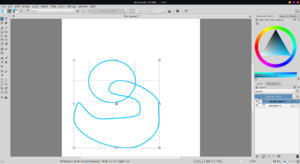

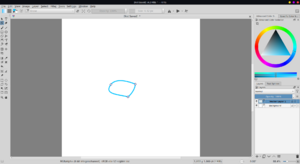
The subtraction tool conditionally works.
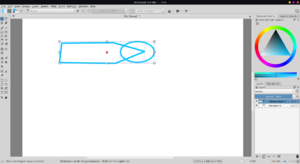
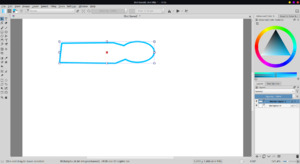
However, it has bugs. It is not perfectly commutative. One order of selection will produce incorrect results, but a different order will produce the correct results. This could lead to missing edges or some extra lines. There are some issues while clipping curves with polygons drawn using polyline tool. However, as these issues do not occur with rectangle tool, these are most certainly bugs, and the algorithm works.
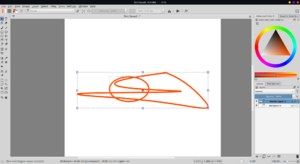
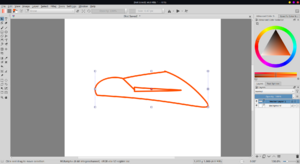
But, if we reselect the shapes, the clipping works as expected
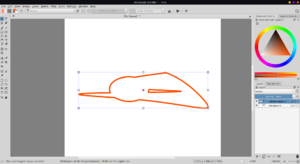
However, as most of the operations do work one way or the other, I guess the algorithm is sound. With some extra time and effort it will produce the correct results. However, given more time, one of the two aforementioned approaches will be a better fit for our purposes as they tend to be cleaner without so many conditions and need for treating the special cases differently.
Ways to complete the remaining task
Current task
I'm currently trying to debug on the clipping algorithm, and write better documentation and improve the coding style.
