GSoC/2021/StatusReports/TanmayChavan: Difference between revisions
m (→Goals) |
(→Links) |
||
| Line 54: | Line 54: | ||
== Links == | == Links == | ||
* MR link: https://invent.kde.org/graphics/krita/-/merge_requests/1002 | |||
* Blog: https://tanmay-chavan.github.io/jasper-blog/ | * Blog: https://tanmay-chavan.github.io/jasper-blog/ | ||
* Project repo: https://invent.kde.org/earendil/bezierintersections (''master branch'') | * Project repo: https://invent.kde.org/earendil/bezierintersections (''master branch'') | ||
Revision as of 17:09, 19 August 2021
Krita - Smarter boolean operations on vector shapes
In Krita, performing boolean operations on vector shapes leads to a large number of unnecessary nodes. This happens because Qt lacks a proper algorithm to find the intersection point of two Bezier curves. I plan on implementing a numerically stable as well as efficient algorithm to find the intersections of two Bezier curves.
Mentors
- Dmitry Kazakov
- Iván Santa María
Goals
- Create a new algorithm to compute intersections of Bezier curves using implicitization
- done!
- Manage the dependencies and implement parts of Qt private modules in Krita codebase
- done!
- Integrate the algorithm with current intersection finding routine
- done!
- Implement the new routine for boolean operations
- not fully done
- Write proper documentation and unit tests for all the above goals while doing them
- ongoing
Status Report
Algorithm for Bezier curve intersection
- This was the exact feature which Qt lacked for boolean operations. As a result, it flattened the curves which in turn made too many nodes. I have implemented an algorithm to compute the intersection points using the implicit representation of a cubic Bezier curve. I have finished implementing curve-curve, line-curve intersections by now. The algorithm works well even with double precision. But, the curve-curve intersections can get really costly. On an average, a single curve-curve intersection-finding routine requires ~280 microseconds. However, it is reported this is the fastest method for curves with degree 5 or less. The line-line intersection point is obtained in the same manner as Qt did.
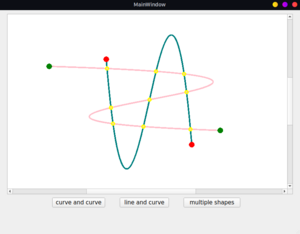
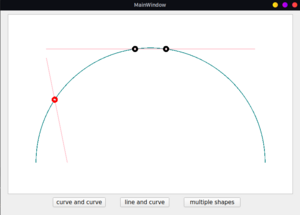
- Relevant links:
- Phabricator task: https://phabricator.kde.org/T14679
- Relevant MRs: https://invent.kde.org/earendil/bezierintersections (Due to the nature of the project, the code can only be merged with Krita codebase upon the entire task being done. Because of this, I have added my work in a seperate toy Qt project which also provides a simple graphic view of the progress until now.)
- Blog post: https://tanmay-chavan.github.io/jasper-blog/jekyll/update/2021/07/13/gsoc-update.html
Qt private dependencies
- As the set operations were handled by the class QPathClipper which lies behind the Qt API, I had to manage the dependencies so that the new implementation would not rely on Qt private modules. This was relatively easy as QPathClipper was fairly independent and it's dependencies didn't have too many dependencies. I also managed to get a downstream copy of the QPainterPath class, albeit had to skip some parts (the PathStroker related part) as it was too closely linked to other Qt private modules. However, it was not required for the purpose of the current tasks. So, I have managed to get the project to run without any private or additional dependencies.
- Relevant links:
- Relevant MRs: https://invent.kde.org/earendil/bezierintersections
- Relevant MRs: https://invent.kde.org/earendil/bezierintersections
Intersection finding routine
- For this, I am using a downstream copy of QPainterPath. The elements of QPainterPaths are extracted and stored in the local version of PainterPath. After this, two vectors for subject shape and clip shape are created, where elements are added with the classes CubicBezier or Line as per the type of elements. Then, it proceeds to find the intersection points between the elements of the two vectors. These are stored in a separate class member with some additional information which could be helpful to perform set operations.
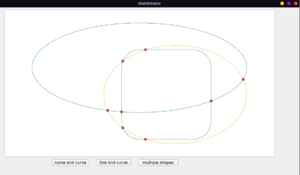
- Relevant links:
- phabricator task: https://phabricator.kde.org/T14681
- Relevant MRs: https://invent.kde.org/earendil/bezierintersections
Shape-clipping algorithm
Clipping proved to be a challenge, and I had initially underestimated it. Most of the problems arose as a suitable implementation was not available online, at least in FOSS. Most of them relied on flattening of the curves, much like Qt's algorithm. The wiki page mentioned Greiner-Hormann algorithm as one possibility for handling clipping for shapes with curves. However, there was no implementation available online. There were also several degenerate cases in Greiner-Hormann. It would fail if the two shapes had common vertices. It will also fail for common/overlapping edges, and for points of intersection lying on the vertices. The solution suggested was to change the co-ordinates of such problematic points. However this might lead to unexpected and undesired results. There is an improved version proposed, but the preprocessing routines were complicated and still had a few drawbacks. If there were a point of intersection coinciding with a point of self-intersection, the shape should be divided into several smaller non-intersecting shapes. Another major issue was that we needed to know at least one vertex of one shape lying outside the other shape. This is implemented in Qt, but within it's API, and works only for lines. (Currently, this can be implemented by using the tight bounding box function, and using an even-odd approach instead of Qt's winding-number approach.)
Apart from this, there was always an uncertainty as it had not been done before. There could be several problems there which remain unknown rill it is implemented. For this reason, I chose not to continue with that approach. However, I am writing down everything that has been done, what remains to be done, and how to do it should one choose to follow this approach.
Links
- MR link: https://invent.kde.org/graphics/krita/-/merge_requests/1002
- Blog: https://tanmay-chavan.github.io/jasper-blog/
- Project repo: https://invent.kde.org/earendil/bezierintersections (master branch)
- Phabricator task: https://phabricator.kde.org/T14574
Current task
I'm currently working on the clipping algorithm. For that, some preprocessing is required for any of the two approaches. I will be able to provide a working demo (although an unoptimized one) in a few days.
