digiKam SoK 2012 Auto Noise Reduction

Sypnosis

digiKam already has a good electronics noise [5] reduction algorithm [3] based on Wavelets theory [6] working in YCrCb color-space [4]. It based on a fork of original implementation of Gimp Denoise tool [1], including several improvements to support 16 bits color depth image and memory leak/bugfixes. Original implementation provides more experimental implementation to support RGB and CIELAB color-spaces to process noise, which have been dropped in digiKam implementation. Only Luminance and Chrominance settings from YCrCB color-space have been preserved because it's the most common way to process electronics noise in digital imagery.

The Wavelets Algorithm implemented in Gimp Denoise Tool is based on DCraw [9] Noise Cleaner code and later ported to Ufraw [10]. The original code from DCraw use an "À Trous" Discrete Wavelet Transform described into "The Handbook of Astronomical Image Processing" book from Richard Berry and James Burnell, chapter 18 [11]. Gimp NR tool author has also re-used this theory to improve original code.

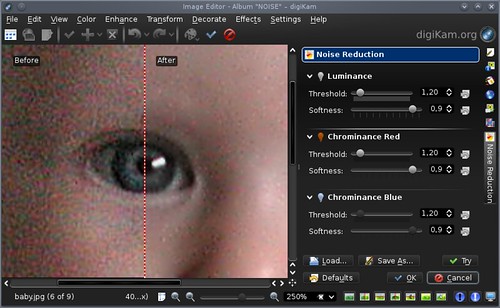full size screenshot from Flickr

digiKam NR tool use manual NR settings. What we need is a Automatic NR settings adjustment option depending upon the input image's noise level and the type of noise present. This would automate the task and will also make it easier for newbies to find the NR settings which 'just works' for the input image.

Closed source program provide a way to compute automatically NR settings accordingly with image contents and camera capture settings, as Sony RAW Image Converter program from Microsoft Windows [7].

Denoise Gimp Tool

The wavelet denoise plugin for The GIMP is an algorithm copied and slightly altered from the UFRaw program (which inherited the algorithm from dcraw). Instead of denoising all RGB channels at once the plugin implementation allows to denoise the RGB channels individually and - even more useful - to denoise the YCbCr or CIELAB channels individually. The colour model conversions are nearly lossless as the internal calculations are done in floating point numbers and rounding errors are avoided.

For camera pictures we advise to use YCbCr mode (which is nearly lossless) and to at least denoise the Cb and Cr channels to reduce the chroma (colour) noise. Cameras shooting in JPEG mode normally have chroma noise already reduced. If desired, the luminance noise can be reduced. This channel usually contains most of the fine structures in the image and should mostly be left alone.

All channels are handled in the same way (regardless of colour space) but independently. One difference to UFRaw and DCRaw algorithm is that It don't use predefined (gaussian) noise level coefficients for each wavelet level, but that It estimate the level by calculating the RMS (Root Mean Square) [12], neglecting image detail. It also use a different "thresholding" function where it specified the "softness" of the threshold.

General goals

Noise level and its type in a image may depend upon various factors such as Camera, ISO and other conditions. A statistical variance between neighboring pixel may give us a rough estimate about the salt & pepper noises. Moreover, this project needs to tested it over a large set of data inorder to get a good relation between detected parameters and settings of wavelet NR.

A simple workflow : from an Input Image we will detect noise level and type of noise; use other info available like camera model, ISO, etc; and to complete, compute Auto Adjust wavelets NR settings.

One of the primary goal is to implement a Noise Level Function (NFL) which works using using a single image [2]. Here in the image data is fit in each region with a smoothing function, then noise is estimated according to the residue remaining. This may over estimate some images which naturally have frequent changes in color, textures, lighting, etc.

Secondly we need to map the obtained Noise Level to the already present NR settings (This would certainly require much of testing with the real image dataset).

Due of lots of different types of electronics noise generated by digital still camera, a collection of noisy images must be collected. A command line test program must be written to check implementation outside digiKam GUI. Some sample files can be already found in digiKam test collection [8].

Project Timeline

Updates

The working model of the nrestimate function with a bit of gui has been posted in https://github.com/Kenzo450D/estimate-noise-image

Todo

Milestone name	Milestone description	Assigned to	Expected Start Date	Status
NLF	Implement the function for Noise estimation as in [2]	Sayantan Datta		Completed
ANR	Adapt the noise levels to the parameters of NR engine	Sayantan Datta		Completed
CDS	Change the code to digiKam style coding	Sayantan Datta		Completed
	Create the files for /core/libs/dimg/filters/nr/nrestimate.xxx	Sayantan Datta		Completed
	Create and test CUI version in /core/tests for stability and bugs	Sayantan Datta		Completed
	Final changes in GUI files	Sayantan Datta	31-oct-2012	Completed
	Documentation	Sayantan Datta		Under Progress